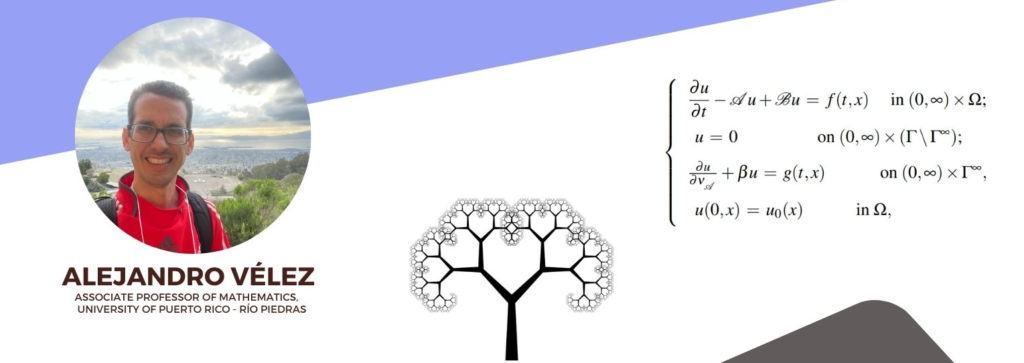
In this talk we deal with the fractal geometry and well-posedness of diffusion equations over a class of domains with ramified boundaries. These domains represent an idealization of the bronchial tree in the respiratory system. We discuss the solvability and global regularity of a generalized diffusion problem over these ramified sets.